 Définition Définition
On appelle hypoténuse, dans un triangle rectangle, le côté
opposé à l'angle droit (le plus grand côté).
 Théorème Théorème
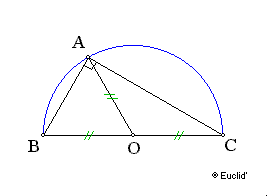
Si A est un point, distinct de B et C, du
cercle de diamètre [BC], alors le triangle ABC est rectangle en A. (d'hypoténuse
[BC])
|
|
 Théorème
Théorème
Si un triangle
est rectangle, alors le centre de son cercle circonscrit est situé au milieu de
son hypoténuse.
Autre formulation
Si un triangle
est rectangle, alors son hypoténuse est un diamètre de son cercle circonscrit.
 Théorème
Théorème
Si
un triangle est rectangle, alors la longueur de la médiane issue de l'angle droit
est égale à la moitié de la longueur de l'hypoténuse.
(et réciproquement).
 Théorème
Théorème
Dans un triangle rectangle, le carré de la longueur de l'hypoténuse
est égale à la somme des carrés des longueurs des côtés
de l'angle droit. Autrement dit :
Si ABC est
un triangle rectangle en A, alors BC2 = AB2 + AC2.
 Exemple
Exemple
ABC
est un triangle rectangle en A tel que AB = 6 cm et BC = 10 cm. Calculer la
longueur du côté [AC].
D'après le théorème de Pythagore appliqué au triangle
ABC rectangle en A, on a :
BC2 = AB2 + AC2
102 = 62 + AC2
100 = 36 + AC2
AC2 = 100 – 36
AC2 = 64
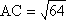
AC = 8
Le côté [AC] mesure 8 cm.
 Théorème (réciproque)
Théorème (réciproque)
Dans un triangle ABC, si BC2 = AB2 + AC2, alors
ABC est un triangle rectangle en A.
 Exemple
Exemple
DEF
est un triangle tel que DE = 5 cm, EF = 12 cm et DF = 13 cm. Est-il rectangle
?
Si le triangle DEF est rectangle, son hypoténuse est nécessairement
[DF] (le plus grand côté)
D'une part
DF2 = 132 = 169
d'autre part
DE2 + EF2 = 52 + 122 = 25 + 144 = 169
Comme DF2 = DE2 + EF2, alors d'après la réciproque du théorème
de Pythagore, le triangle DEC est rectangle en E.
 Théorème (contraposée)
Théorème (contraposée)
Dans un triangle ABC, si BC2 ¹ AB2 + AC2 (où
[BC] est le plus grand côté), alors le triangle ABC n'est pas rectangle.
 Exemple
Exemple
RST est un triangle tel que RS = 3,7 cm, ST = 7,1 cm et RT = 8,1 cm. Est-il
rectangle ?
Si le triangle RST est rectangle, son hypoténuse est nécessairement
[RT] (le plus grand côté)
D'une part
RT2 = 8,12 = 65,61
d'autre part
RS2 + ST2 = 3,72 + 7,12 = 13,69 + 50,41 = 64,1
Comme RT2 ¹ RS2 + ST2, alors d'après la controposée
du théorème de Pythagore, le triangle RST n'est pas rectangle.
![]() Définition
Définition![]() Théorème
Théorème