

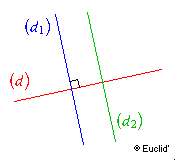
Si (d1) // (d) et (d2) // (d),
alors (d1) // (d2)
Si (d1) ^ (d) et
(d2) ^ (d),
alors (d1) // (d2)
Si (d1) // (d2) et
(d1) ^ (d),
alors (d) ^
(d2)
PARALLÉLISME |
Accueil
| L'Essentiel | Les Annales
| Hors
Programme | Documents
| Logiciels |
Bibliographie | Liens
| Livre d'Or |
Aires et Périmètres | Parallélisme | Droites du triangle
| Distance | Transformatins du Plan |
Propriétés des parallèles et des perpendiculaires |
|
|
|
Si (d1) // (d) et (d2) // (d), |
Si (d1) ^ (d) et
(d2) ^ (d), |
Si (d1) // (d2) et
(d1) ^ (d), |
Angles avec une sécante |
![]() Définition
Définition
Deux
angles sont dits complémentaires, si la somme de leur mesure est égale à
90°
![]() Définition
Définition
Deux
angles sont dits suppléméntaires, si la somme de leur mesure est égale à
180°
Angles opposés par le
sommet :
a1 et a3, a2
et a4, b1
et b3, b2
et b4
|
|
![]() Théorème
Théorème
Si les droites
(d1) et (d2) sont parallèles,
alors les couples d'angles définis en ![]() ,
, ![]() et
et ![]() ont, deux
à deux, la même mesure.
ont, deux
à deux, la même mesure.
![]() Théorème
Théorème
Si deux des
angles définis en ![]() ,
, ![]() et
et ![]() ont, deux
à deux, la même mesure, alors les droites
(d1) et (d2) sont parallèles.
ont, deux
à deux, la même mesure, alors les droites
(d1) et (d2) sont parallèles.
Droite des milieux d'un triangle |
|
|
|
|
Théorème de Thalès |
![]() Définition
Définition
Deux
triangles ABC et ADE forment une configuration
de Thalès si les points (A, B,
D) et (A, C, E) sont alignés dans le même ordre
|
|
|
Configurations "Triangles emboîtés" |
Configuration "Papillon" |
|
![]() Théorème
Théorème
Si les triangles
ABC et ADE forment une configuration de
Thalès et si les droites
(BC) et (DE) sont parallèles, alors![]() (Les triangles ABC et ADE sont à côtés proportionnels.)
(Les triangles ABC et ADE sont à côtés proportionnels.)
![]() Théorème
(réciproque)
Théorème
(réciproque)
Si les triangles
ABC et ADE forment une configuration de Thalès et
si ![]() , alors
les droites (BC) et (DE) sont parallèles
, alors
les droites (BC) et (DE) sont parallèles
![]() Théorème
(contraposée)
Théorème
(contraposée)
Si les triangles ABC et ADE forment une configuration de Thalès
et si ![]() , alors les droites (BC) et (DE) ne sont pas parallèles
, alors les droites (BC) et (DE) ne sont pas parallèles
Ensemble de points |
Ensemble des points M,
d'une droite (AB) donnée, tel que : |
|
Accueil
| L'Essentiel | Les Annales
| Hors
Programme | Documents
| Logiciels |
Bibliographie | Liens
| Livre d'Or |