REPÈRES ORTHONORMÉS DU PLAN

Accueil | L'Essentiel | Les Annales | Hors Programme | Documents  | Logiciels | Bibliographie | Liens | Livre d'Or

Aires et Périmètres | Parallélisme | Droites du triangle | Distance | Transformatins du Plan
Angles et Trigonométrie | Triangle rectangle | Repères orthonormés du plan | Quadrilatères | Volumes 

 



Coordonnées d'un point

 

Définition
Un repère orthonormé (ou orthonormal) est un ensemble de deux axes, (xx') et (yy'), gradués avec la même unité (OI = OJ = 1 unité), perpendiculaires et ayant la même origine O.
On le note (O ; I ; J)
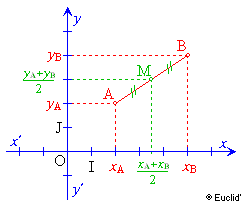
M a pour abscisse xM = 2 et pour ordonnée yM = 3.
On note ses coordonnées M(2 ; 3)

 

Points particuliers
O (0 ; 0) : origine du repère
I (1 ; 0)  : point définissant l'unité sur l'axe des abscisses.
J ( 0 ; 1) : point définissant l'unité sur l'axe des ordonnées.

 

Coordonnées du milieu d'un segment


Règle : 

Exemple
Soient A (2 ; 2) et B (5 ; 4), calculer les coordonnées de M milieu de [AB]


 M (3,5 ; 3)

 

 

 

Coordonnées d'un vecteur


Règle :

  Exemple
Soient A (2 ; 2) et B (5 ; 4). Calculer les coordonnées du vecteur
(xB – xA ; yB – yA)
(5 – 2 ; 4 – 2)
 (3 ; 2)

 

 

 

Distance dans un repère orthonormé


Règle :

  Exemple
Soient A (2 ; 2) et B (5 ; 4). Calculer AB.

 

 

 

 

Accueil | L'Essentiel | Les Annales | Hors Programme | Documents  | Logiciels | Bibliographie | Liens | Livre d'Or