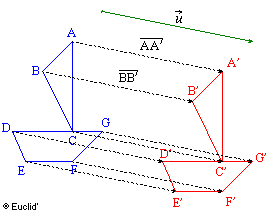
Définition Définition
A et A' sont symétriques par rapport à
une droite (D), si (D) est la médiatrice
du segment [AA']
 Définition Définition
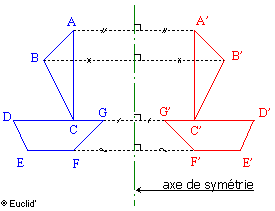
Une droite (d) est un axe de symétrie pour
une figure, si tout point de cette figure a son image sur elle-même.
|
|
 Définition Définition
A et A' sont symétriques par rapport à
un point O, si O est le milieu du segment [AA'].
 Définition Définition
O est un centre de symétrie pour une figure,
si tout point de cette figure a son image sur elle-même.
|

|
 Théorème
Théorème
Si 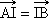 , alors I est le milieu de [AB] (et réciproquement).
, alors I est le milieu de [AB] (et réciproquement).
 Règle
Règle
Le point D, tel que 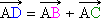 ,
est le 4ème sommet du parallélogramme ABDC.
,
est le 4ème sommet du parallélogramme ABDC.
 Règle
(Relation de Chasles)
Règle
(Relation de Chasles)
Quels que soient les points A, B et C, on a : 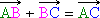
 Définition
Définition
Les deux vecteurs 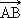 et
et 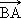 sont opposés. Ils ont la même direction, la même
longueur, mais des sens contraires :
sont opposés. Ils ont la même direction, la même
longueur, mais des sens contraires : 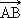 +
+ 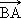 =
= 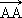 =
= 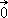 (vecteur nul).
(vecteur nul).
 Théorème
Théorème
La composée d'une translation de vecteur  et d'une translation de vecteur
et d'une translation de vecteur 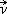 est une translation de vecteur
est une translation de vecteur  +
+ 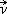 .
.
 Théorème
Théorème
La composée d'une symétrie centrale de centre I
et d'une symétrie centrale de centre J, est une translation de vecteur
2  .
.
 Définition Définition
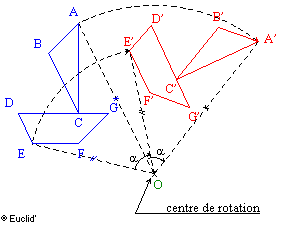
On dit que A' est l'image de A par la rotation de
centre O et d'angle a si OA' = OA et 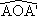 = a. = a.
 Définition Définition
On appelle sens
direct, sens positif
ou sens trigonométrique, le sens contraire des aiguille d'une montre.
 Théorème Théorème
Une symétrie centrale est une rotation d'angle
180° (le sens peut être direct ou indirect.)
|
|
 Caractéristique
d'un polygone régulier Caractéristique
d'un polygone régulier
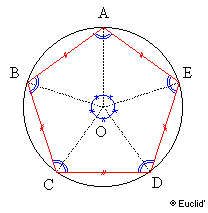
– Il est inscriptible dans un cercle.
– Tous les côtés
ont la même longueur.
– Les angles au centre ont la même
mesure.
– Les angles aux sommets ont la même mesure.
 Définition Définition
Un polygone qui vérifie 2 des 4 caractéristiques
précédentes, vérifie nécessairement
les 2 autres et, est appelé
polygone régulier.
|
|
 Propriétés
Propriétés
– Un polygone régulier est invariant par rotation de
centre, le centre du cercle circonscrit et d'angle un multiple de la mesure
d'un angle au centre.
– Si on considère un polygone régulier à n côtés alors la mesure d'un angle au centre est égale
à 360 / n et celle d'un angle au sommet est égale à 180
– 360 / n.
 Principaux polygones réguliers
Principaux polygones réguliers
n |
nom |
angle au centre |
angle au sommet |
3 |
triangle équilatéral |
120° |
60° |
4 |
carré |
90° |
90° |
5 |
pentagone régulier |
72° |
108° |
6 |
hexagone régulier |
60° |
120° |
7 |
heptagone régulier |
»
51.43° |
»
128.57° |
8 |
octogone régulier |
45° |
135° |
9 |
ennéagone régulier |
40° |
140° |
10 |
décagone régulier |
36° |
144° |
11 |
hendécagone régulier |
»
32.73° |
»
147.27° |
12 |
dodécagone régulier |
30° |
150° |
15 |
pentadécagone régulier |
24° |
156° |
n |
n-gone |
360 / n |
180 – 360 / n |
 Cas particulier
Cas particulier
Dans un hexagone régulier (6 côtés), la longueur
d'un côté est égale au rayon du cercle circonscrit.
Propriétés des isométries
(symétries, translations et rotations) |
![]() Définition
Définition![]() Définition
Définition