Problème
Un club de gymnastique propose, pour l'utilisation de ses installations, les trois tarifs suivants :
Tarif A : 80 F par séance.
Tarif B : abonnement annuel de 1 000 F, puis 40 F par séance.
Tarif C : forfait annuel de 3 000 F donnant droit à autant de séances que l'on désire.
 

Partie A

1. Recopier et compléter le tableau suivant.

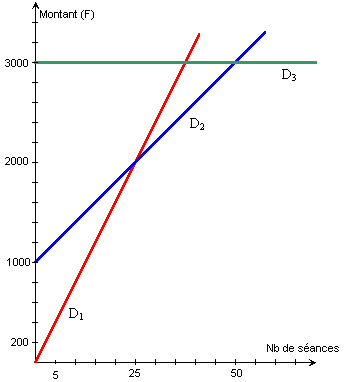
2. Exprimer, en fonction du nombre x de séances annuelles :
    a. Le coût P_A pour un utilisateur ayant choisi le tarif A.
    b. Le coût P_B pour un utilisateur ayant choisi le tarif B.
3. Une personne désire dépenser 2 400 F dans l'année pour l'utilisation des installations de ce club. A combien de séances aura-t-elle droit si elle choisit le tarif B ?

4. Soit l'inéquation 80x < 1 000 + 40x.
    a. La résoudre.
    b. Donner une interprétation du résultat trouvé.

Partie B

le plan est muni d'un repère orthogonal.
On consacrera une page entière au graphique et on placera l'origine O du repère en bas à gauche de la feuille.
– Sur l'axe des abscisse, 1 cm représentera 5 unités.
– Sur l'axe des ordonnées, 1 cm représentera 200 unités.

1. Tracer les droites :
     D₁ d'équation y = 80x
     D₂ d'équation y = 40x + 1 000
     D₃ d'équation y = 3 000

 2. Une personne dispose de 1 600 F pour l'utilisation des installations de ce club.
     Déterminer graphiquement le nombre de séances auquel elle pourra participer :
     a. si elle choisit le tarif A.
     b. si elle choisit le tarif B.
(On fera clairement apparaître sur le graphique les traits utilisés.)

3. Soient M le point d'intersection des droites D₁ et D₂, et N celui des droites D₂ et D₃.
     a. Lire sur le graphique les coordonnées de M
     b. Calculer les coordonnées de N.

4. Déterminer graphiquement, selon le nombre de séances annuelles, le tarif de plus avantageux.
 

Corrigé

Commentaires

Partie A

1. Recopier et compléter le tableau suivant.

2. Exprimer, en fonction du nombre x de séances annuelles :
    a. Le coût P_A pour un utilisateur ayant choisi le tarif A.

    b. Le coût P_B pour un utilisateur ayant choisi le tarif B.

3. Une personne désire dépenser 2 400 F dans l'année pour l'utilisation des installations de ce club. A combien de séances aura-t-elle droit si elle choisit le tarif B ?

P_B = 40x + 1000
Il faut donc résoudre l'équation : 40x + 1 000 = 2 400

   40x + 1 000 = 2 400
   40x + 1 000 – 1 000 = 2 400 – 1 000
   40x = 1 400 
   40x / 40 = 1 400 / 40

 Pour 2 400 F avec le tarif B, elle aura droit à 35 séances.
 

4. Soit l'inéquation 80x < 1 000 + 40x.
    a. La résoudre.

   80x < 1 000 + 40x
   80x – 40x < 1 000 + 40x – 40x
   40x < 1 000
   40x / 40 < 1 000 / 40

    b. Donner une interprétation du résultat trouvé

80x < 1 000 + 40x correspond à P_A < P_B

Ce résultat correspond aux nombres de séances (x < 25) pour lesquels le tarif A est plus avantageux que le tarif B.
 

Partie B  

1. Tracer les droites :
     D₁ d'équation y = 80x [en rouge]
     D₂ d'équation y = 40x + 1 000 [en bleu]
     D₃ d'équation y = 3 000 [en vert]

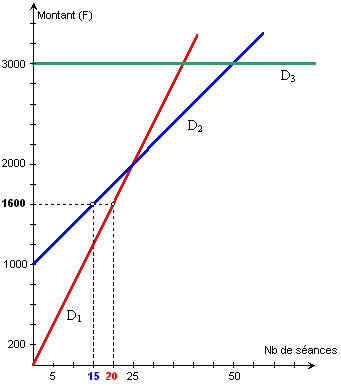
2. Une personne dispose de 1 600 F pour l'utilisation des installations de ce club. Déterminer graphiquement le nombre de séances auquel elle pourra participer :

     a. si elle choisit le tarif A.

Si elle choisit le tarif A elle pourra bénéficier de 15 séances

     b. si elle choisit le tarif B.

Si elle choisit le tarif B elle pourra participer à 20 séances

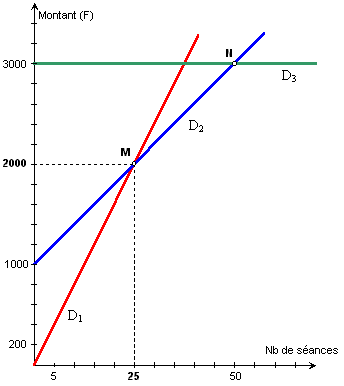
3. Soient M le point d'intersection des droites D₁ et D₂, et N celui des droites D₂ et D₃.
     a. Lire sur le graphique les coordonnées de M

En lisant le graphique on obtient : M (25 ; 2000)

     b. Calculer les coordonnées de N.

   40x + 1 000 = 3 000
   40x + 1 000 – 1 000 = 3000 – 1 000
   40x = 2 000
   40x / 40 = 2 000 / 40

Les coordonnées du point N sont N(50 ; 3 000)
 

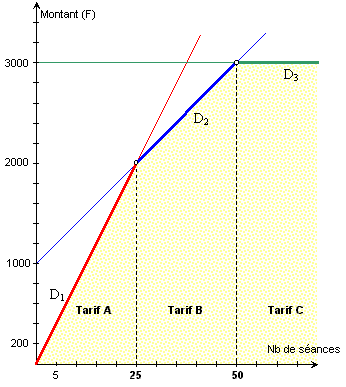
4. Déterminer graphiquement, selon le nombre de séances annuelles, le tarifs de plus avantageux.

En dessous de 25 séances annuelles il vaut mieux prendre le tarif A
Entre 25 et 50 séances, le tarif B est plus économique.
Au delà de 50 séances, C est le tarif le plus rentable.