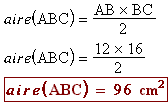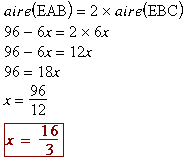Problème |
|
ABC est un triangle tel que : |
|
Partie I 1. Démontrer que le triangle ABC
est rectangle en B. [ 1
pt ] Partie II On se place dans le cas où CF = 4 cm. Partie III On se place dans le cas où F est un point
quelconque du segment [BC], distinct de B et de C. |
|
Corrigé |
Commentaires |
Partie I 1. Démontrer que le triangle ABC est
rectangle en B. |
|
2. Calculer l'aire du triangle ABC. |
|
3. Démontrer, en s'aidant de la question
1. que la droite (EF) est parallèle à la droite (AB). |
|
Partie II (CF = 4 cm) |
|
2. Calculer l'aire du triangle EBC. |
|
Partie III (CF = x ) |
|
2. Montrer que l'aire du triangle EBC, exprimée
en cm², est égale à 6x.
|
|
3. Pour quelle valeur de x
l'aire du triangle EBC , exprimée en cm², est-elle égale
à 33 |
|
4. Exprimer en fonction de x
l'aire du triangle EAB. Pour quelle valeur exacte de x
l'aire du triangle EAB est-elle égale au double de l'aire
du triangle EBC ? Pour |