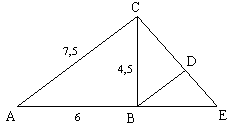
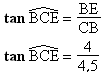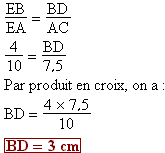Exercice 2

On considère la figure ci-contre :
On donne AB = 6 cm ; AC = 7,5 cm ; BC = 4,5 cm (sur le schéma, les dimensions ne sont pas respectées).
E est le point de [AB) tel que AE = 10 cm.
La parallèle à (AC) passant par B coupe (CE) en D.
1. Démontrer que le triangle ABC est rectangle en B.
2. Calculer la valeur arrondie au degré de la mesure de l'angle .
3. Déterminer la mesure du segment [BD].  

Corrigé

Commentaires

1. Démontrer que le triangle ABC est rectangle en B

D'une part : AC² = 7,5² = 56,25
D'autre part AB² + BC² = 6² + 4,5² = 36 + 20,25 = 56,25
Comme AC² = AB² + BC² , alors d'après la réciproque du théorème de Pythagore, le triangle ABC est rectangle en B.

2. Calculer la valeur arrondie au degré de la mesure de l'angle .

Le point B appartient au segment [AE], donc BE = AE – AB = 10 – 6 = 4 cm. De plus le triangle BCE est rectangle en B, donc :

La calculatrice donne » 42° (valeur arrondie au degré près)
 

3. Déterminer la mesure du segment [BD].

Les points E, B, A sont alignés, les points E, D, C sont alignés dans le même ordre et les droites (AC) et (BD) sont parallèles, donc d'après le théorème de Thalès, on a :