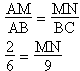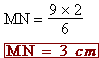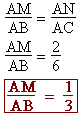Corrigé |
Commentaires |
1. Résoudre
le système :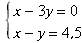
La première équation
peut s'écrire x = 3y.
En remplaçant dans la deuxième on obtient
3y – y = 4,5
2y
= 4,5
y = 2,25
et
x = 3y
x
= 3 × 2,25
x = 6,75.
La solution du système est (6,75
; 2,25)
|
[ Systèmes d'équations ]
[ Méthode de substitution ]
|
2. a.
Calculer MN
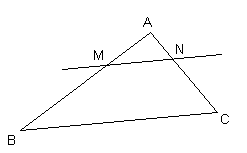
Les points A,M,B et A,N,C
sont alignés dans le même ordre, donc les triangles
AMN et ABC forment une configuration de Thalès.
Comme
les droites (MN) et (BC) sont parallèles, alors d'après
le théorème de Thalès, on a :
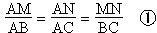
A l'aide de cette égalité,
on peut écrire :
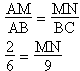
D'où
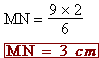
|
[ Configuration de Thalès ]
[ Théorème de Thalès ]
|
2. b. Donner la valeur de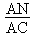
D'après l'égalité  ,
on a : ,
on a :
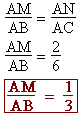
|
|
3. a.
Établir les égalités : x – y = 4,5 et x
– 3y = 0
Comme le point N appartient au segment [AC], alors
AN + NC = AC.
Soit AC – AN = NC
D'après
la question 2.b. on a :
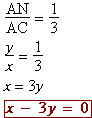
|
|
3. b.
Calculer AN et AC
AN et AC vérifient le système
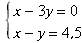 , dont les solutions, d'après
la question 1. sont x
= 6,75 et y = 2,25 , dont les solutions, d'après
la question 1. sont x
= 6,75 et y = 2,25
D'où
|
|