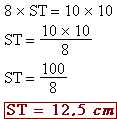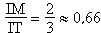Exercice 2
Sur la figure ci-contre, tracée à main levée :
IR = 8 cm ; RP = 10 cm ; IP = 4,8 cm ; IM = 4 cm
IS = 10 cm ; IN = 6 cm ; IT = 6 cm
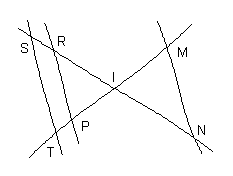
(On ne demande pas de refaire la figure.)

1. Démontrer que les droites (ST) et (RP) sont parallèles [ 1,5 pt ]
2. En déduire ST [ 1 pt ]
3. Les droites (MN) et (ST) sont-elles parallèles ? Justifier [ 1,5 pt ]

Corrigé

Commentaires

1. Démontrer que les droites (ST) et (RP) sont parallèles

Les points I, R, S et I, P, T sont alignés dans le même ordre, donc les triangles IRP et IST forment une configuration de Thalès.
D'une part

D'autre part
 
Comme , alors d'après la réciproque du théorème de Thalès, les droites (ST) et (RP) sont parallèles.
 

2. En déduire ST

Dans la configuration de Thalès citée à la question 1, comme les droite (ST) et (RP) sont parallèles, d'après le théorème de Thalès, on a :


Par produit en croix :

 3. Les droites (MN) et (ST) sont-elles parallèles ? Justifier

Les points S, I, M et T, I, M sont alignés dans le même ordre, donc les triangles IST et INM forment une configuration de Thalès "papillon". 
D'une part

d'autre part

Comme , alors d'après la contraposée du théorème de Thalès, les droites (MN) et (ST) ne sont pas parallèles.