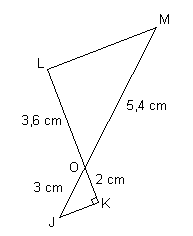
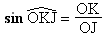Exercice 1
1. Calculer l'angle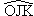 (on donnera l'arrondi au degré
près) (on donnera l'arrondi au degré
près)
Dans le triangle OJK, rectangle en K, on a
:
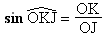

La calculatrice donne
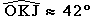 valeur arrondie
au degré. valeur arrondie
au degré.
|
Sinus = opposé
/ hypoténuse
[ Sinus
]
|
2. Démontrer que les droites (JK)
et (LN) sont parallèles
Les points K, O, L et J,
O, N sont alignés dans le même ordre, donc, les triangles
OKJ et OLN forment une configuration de Thalès "papillon".
D'une part :
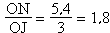
d'autre part :
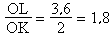
Comme 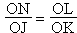 , alors, d'après la
réciproque du théorème de Thalès, les
droites (LN) et (JK) sont parallèles. , alors, d'après la
réciproque du théorème de Thalès, les
droites (LN) et (JK) sont parallèles.
|
[ Configuration de Thalès ]
[ Réciproque du théorème
de Thalès ]
|
3. Déduire de la question 2. sans effectuer
de calculs, que les angles 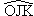 et et 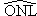 sont égaux sont égaux
Les angles 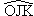 et et 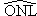 sont des angles alternes-internes et comme les droites (LN) et (JK)
sont parallèles, alors ils ont la même mesure.
sont des angles alternes-internes et comme les droites (LN) et (JK)
sont parallèles, alors ils ont la même mesure.
|
Souvenirs de la classe de cinquième...
[ Angles alternes-internes ]
|