Accueil
| L'Essentiel | Les Annales
| Hors
Programme | Documents
| Logiciels |
Bibliographie | Liens | Livre d'Or |
Introduction : Le mot hypothèse possède divers sens, qu'il ne faut pas confondre.
Hypothèse
n. f.
1. (MATH) Point de départ d'une démonstration
logique, posé dans l'énoncé et à partir duquel on
se propose d'aboutir à la conclusion.
2. (Dans les sciences expérimentales.) Explication
plausible d'un phénomène naturel, provisoirement admise et destinée
à être soumise au contrôle méthodique de l'expérience.
Hypothèse confirmée, infirmée par l'expérience.
3. (Sens courant.) Supposition, conjecture que l'on fait
sur l'explication ou la possibilité d'un événement. Émettre
une hypothèse.
(Source : Dictionnaire HACHETTE multimédia
encyclopédique 97)
Les questions qu'on doit se poser : 1 Que cherche-t-on à démontrer ? (La conclusion) 2 Quels
sont les éléments dont on dispose ? 3 Quels sont les propriétés ou théorèmes que l'on connaît et qui ont un rapport avec l'énoncé ? |
![]() La réalisation,
en géométrie, d'une figure d'étude est indispensable. Ne
pas oublier de bien la coder. Cette figure permet d'avoir l'essentiel sous les
yeux (mais pas toujours tout).
La réalisation,
en géométrie, d'une figure d'étude est indispensable. Ne
pas oublier de bien la coder. Cette figure permet d'avoir l'essentiel sous les
yeux (mais pas toujours tout).
![]() La recherche
d'une démonstration se fait "à l'envers". On part de
la conclusion, et on "remonte", de proche en proche, jusqu'à
arriver aux informations (données ou hypothèses) dont on dispose
dans l'énoncé.
La recherche
d'une démonstration se fait "à l'envers". On part de
la conclusion, et on "remonte", de proche en proche, jusqu'à
arriver aux informations (données ou hypothèses) dont on dispose
dans l'énoncé.
ATTENTION :
Il ne faut jamais utiliser, dans une démonstration, la conclusion comme
étant supposée vraie. La conclusion n'apparaît qu'à
la fin.
![]() La rédaction
de la démonstration, quant à elle, se fait dans le "bon"
sens.
La rédaction
de la démonstration, quant à elle, se fait dans le "bon"
sens.
Pour cela, on utilise une rédaction du style :
Comme Hypothèse(s) , alors Conclusion(s)
D'après Hypothèse(s) , on a Conclusion(s)
On a Hypothèse(s) , donc Conclusion(s)
Comme Hypothèse(s) du Théorème, alors d?après Théorème, Conclusion(s) du Théorème
(Quand on utilise un théorème, il ne faut pas oublier d'en vérifier les conditions d'utilisation. C'est à dire qu'on a TOUT ce qu'il faut pour pouvoir l'utiliser.)
![]() On utilise
aussi des liens tels que :
On utilise
aussi des liens tels que :
Par suite, Par conséquent, Il s'ensuit que, Il en résulte que,
Il en découle, On en déduit que, On obtient, De plus, En outre,
etc.
![]() Plus une rédaction
est aérée, plus elle est facile à lire et à comprendre.
Dans la mesure du possible, il vaut mieux éviter les phrases longues.
Ne pas hésiter à retourner à la ligne.
Plus une rédaction
est aérée, plus elle est facile à lire et à comprendre.
Dans la mesure du possible, il vaut mieux éviter les phrases longues.
Ne pas hésiter à retourner à la ligne.
![]() Le vocabulaire
utilisé doit être précis
Le vocabulaire
utilisé doit être précis
Ex. : les mots centre et milieu ne sont pas des synonymes
dans le langage mathématique, de même pour aire-surface,
chiffre-nombre, sens-direction, contraire-opposé-inverse,
cercle-disque.
![]() Ne
pas mettre d'abréviations dans les phrases.
Ne
pas mettre d'abréviations dans les phrases.
On écrit soit "les droites (AB) et (CD) sont perpendiculaires",
soit "on a (AB) ^ (CD)", mais pas
"les droites (AB) et (CD) sont ^ ".
![]() Ne
pas confondre les notations
Ne
pas confondre les notations
AB : longueur du segment [AB].
[AB] : segment d'extrémités A et B.
(AB) : droite contenant les points A et B.
[AB) : demi-droite d'origine A et contenant le point B.
[BA) : demi-droite d'origine B et contenant le point A.
![]() : vecteur d'origine A et d'extrémité B.
: vecteur d'origine A et d'extrémité B.
= : égalité entre deux expressions
» : approximation
(valeur approchée).
Écrire AB ^ CD n'a pas de sens.
[AB] = [CD] n'est vrai que si les points A et C d'une part, B et D d'autre part,
sont confondus (ou A et D d'une part, B et C d'autre part)
![]() Les
phrases qui utilisent les mots "car", "parce que" ou "puisque"
sont à évitées. Elles nécessitent de mettre la conclusion
avant les hypothèses. (La charrue avant les bufs !)
Les
phrases qui utilisent les mots "car", "parce que" ou "puisque"
sont à évitées. Elles nécessitent de mettre la conclusion
avant les hypothèses. (La charrue avant les bufs !)
![]() Se méfier des
"on voit que". Un dessin constitue très
rarement une preuve.
Se méfier des
"on voit que". Un dessin constitue très
rarement une preuve.
Exemple de démonstration |
Énoncé : ABC est un triangle rectangle
en B et I est le milieu de son hypoténuse. |
Au brouillon Recherche de la démonstration (L'essentiel du travail !)
Figure d'étude :
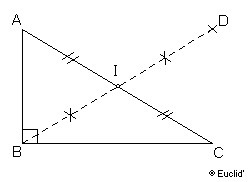
Hypothèses : (Données du problème) 1 ABC triangle rectangle en B |
Conclusion : ABCD est un rectangle |
Propriétés ayant un rapport avec l'énoncé :
Un rectangle est un parallélogramme qui possède un angle
droit.
Un parallélogramme a ses diagonales qui se coupent en leur milieu.
Si A et B sont symétriques par rapport à I alors I est le milieu
du segment [AB].
Schéma de démonstration :
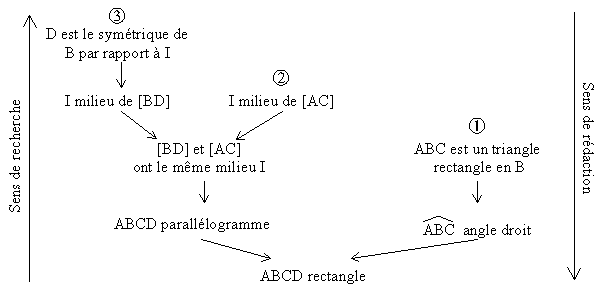
Sur la copie Rédaction de la démonstration
· Les points B et D sont symétriques par rapport à I, donc I est le milieu du segment [BD].
· Par énoncé, I est aussi le milieu du segment [AC].
· Comme le quadrilatère ABCD a ses diagonales [AC] et [BD] qui se coupent en leur milieu I, alors c'est un parallélogramme.
· De plus, le triangle
ABC est rectangle en B, donc l'angle ![]() est droit.
est droit.
· Par conséquent le parallélogramme ABCD est un rectangle.
q.e.d.
Remarque : La rédaction proposée ci-dessus ne prétend pas être LA rédaction, mais UNE rédaction possible (qui a le mérite d'être complète) parmi d'autres.
Accueil
| L'Essentiel | Les Annales
| Hors
Programme | Documents
| Logiciels |
Bibliographie | Liens | Livre d'Or |